Part Seven

[Note: September 2024 - Elsinore Mk6 is current - some things may be  obsolete]

Gathering Acoustic & Z Data

The following page was written with Mark 1 Elsinores in mind:

Methodology: Treat whole system as a Point Source, measure and gather data as such. This results in validated data that can be modelled with greater accuracy. It minimises potential errors during this phase, and since the electrical data is real and the acoustic measurements are all amplitude and phase related at a single point (as represented by the position of the microphone).

As happens with this kind of project, things start slowly and deliberately, much checking and double-checking. Gradually it gathers momentum, especially at the point where the cabinets are made. If you have not covered every base and have in mind exactly where you are going, then we could face a mini-disaster. At the end it becomes quite a rush and a mass of activity.

(Old Mk1 Elsinores)

More Photos of Construction...

Re the whole concept (which includes a number of sub-sets of concepts), I admit at the outset there were some nagging concerns. But I went over and over the issues, both in mind and also using my trusty calculator and using a reliable CAD program and other suitable tools. You’d be surprised how useful a 2D graphic CAD program can be in checking angles and measure diagonal lengths that would be a headache otherwise. You will see an example shortly.

It’s been two years since the initial sketching and to see things coming together at the end and realise you did get enough of the details right not to end up with a mess that simply doesn’t work, and the end result has lived up to expectations, is both a relief and a quiet exhilaration. Here is a diagram generated by my trusty CAD program. We shall refer to this diagram as the discussion furthers.

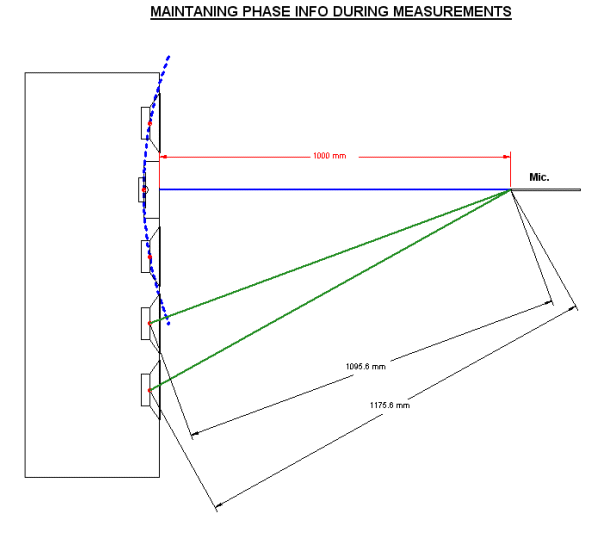
(These were also checked and modelled at 2 Metre)

OK, where to go from here? I suppose "Raw Measurements." This is basically the data you need to accumulate so computer modelling can be a reality. Here the simple rule is this: They must be accurate and with acoustic measurements, the relative phase measurements must be maintained.

The above diagram now allows us to model the whole system as a Point Source. This is despite the fact that the whole system is not a point source (note the bottom two drivers), but in the modelling process it assumes that all drivers are and thus does not change the position of the drivers when modelling. Amplitude and phase relationships are maintained and the electrical measurement (impedance and impedance phase) are real measurements, thus the software can use all three sets of data accurately when components are inserted between the zero Ohm impedance of the amplifier (although the affect of changing that can be modelled as well) and the speakers in situ (the box).

All data must be collected in the box (electrical) and from the box (acoustic) - a real box.

The Process:

Microphone: Exactly 1 Metre from the Front Panel proper on Tweeter Axis, see solid Blue Line.

Note that the top three drivers are equidistant from the Mic. This means that on the Tweeter Axis the top three drivers approximates a point source. But the bottom two drivers are different distances, one being 1095mm and the other 1175mm. They will not be point source, but ignore this.

We shall make the following acoustic measurements:

1. Tweeter: We shall apply a calibrated pulse method (called MLS) signal to the Tweeter that equates to 2.83V – the standard equivalent to 1 Watt into 8 Ohm.

2. Top Two Bass/Mid Drivers: The same measurements but these two drivers are connected in series and as such provide a 16 Ohm load to the same 2.83V test signal.

3. Bottom Two Bass/Mid Drivers: Measured exactly in the same way, also series and 2.83V etc.

Even though only taken at 1 Metre, these are called Farfield measurements.

In this way we are able to capture the relative phase relationship between all the drivers. This will ensure that the modelling program will accurately sum the drivers correctly. It also greatly reduces the complexities when we reach that stage, a classic KISS situation.

But we shall stay with the ON axis measurements for simplicity’s sake and later revisit of the OFF axis.

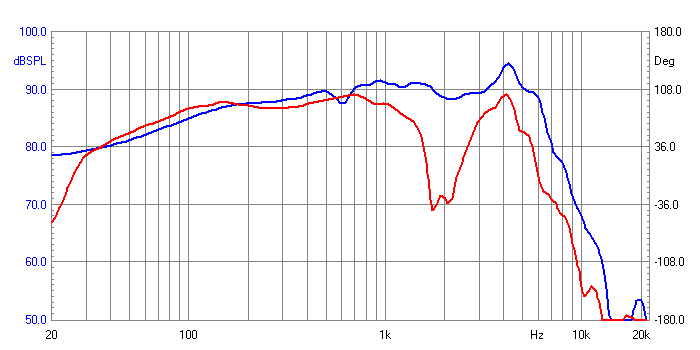
1 Metre ON Axis Farfield Responses - Blue is Mid-Bass & Red is Bottom Bass

These drivers sum perfectly as a single driver at the Mic position. The Red Line represents the bottom two Bass/Mid drivers. They show a major dip in the response centred on 2KHz. This is to be expected as the pulses arrive at different times. Look at the following:

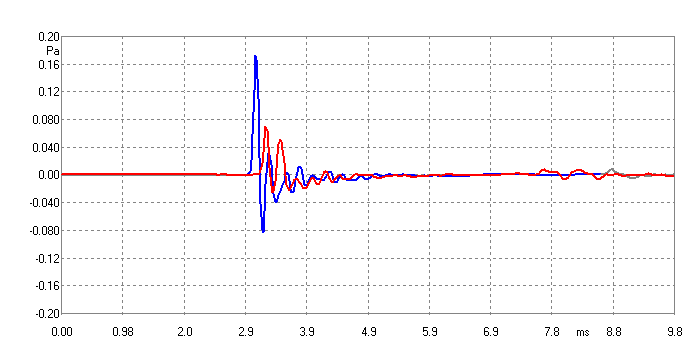
Farfield Impulses (these are ON Axis) - Blue is Mid-Bass & Red is Bottom Bass

The Blue Line here represents the top drivers. Note how they sum into a single and large pulse. The Red Line represents the bottom drivers. There are now two smaller pulses arriving at the Mic at different and later times. They cannot sum up as a larger single pulse even though they contain the same combined energy even though the individual pulses are only about half the peak. Our first diagram allows us to calculate the difference between the delays (actually the pulse graph does as well by looking at the time difference between the pulses) and it is 80mm approx.

This 80mm is the same as the wavelength of 4KHz approx. So the halve-wavelength is 2KHz – and halve-wavelength equals 180° phase shift and hence large cancellation at 2Khz.

It is not as bad as it looks, not by a long shot. I don’t know about you, but I don’t listen to speakers at 1 Metre. So going back to my trusty 2D CAD and using the same technique, at a distance of 2.5M becomes 35mm and the dip up to 5KHz. As we shall be rolling the bottom drivers off slowly above a few hundred Hertz, this all becomes inconsequential. Ignore the dip.

The other observation, in the responses above, ignores the curve below 200 Hertz. They are inaccurate as we have windowed the pulse. Here is an example:

Windowed Pulse

Note it has been cut of before the ‘wriggle’ (that is the reflection caused by the floor between the speaker and the Mic) and also the delay before the pulse. We can see the window is about 6 milliseconds, so it is only valid down to 1/0.006 = 166 Hertz. (Actually we will not window/edit time before the pulse as we need that for modelling later).

We shall later use Nearfield measurements to fill in the missing data. But Farfield gives us most of the valid data, including the critical phase relationships and also the correct SPL data.

Now let us take a look at the Tweeter’s acoustic response:

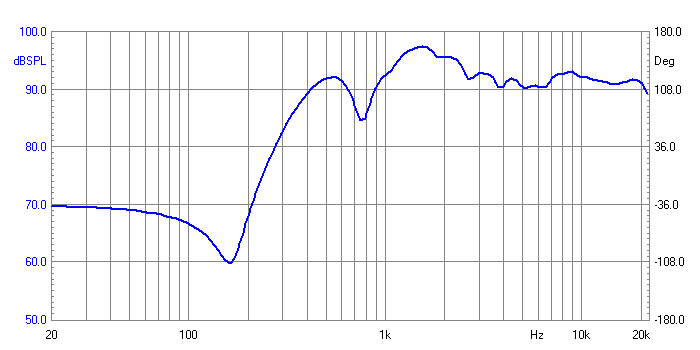
Tweeter ON Axis Response

Again ignore data below 200 Hertz. This response contains considerable features. But to understand them, please take a look at what I have called the Diffraction Wedge that surrounds the Tweeter. This is required as the Tweeter sits fairly deep into a cavity. If left like that the response would look quite horrible. I may at a later stage show you what it looked like, but I need to maintain continuity here. Take a look at the photo:

Here are the same responses as above but at 25° OFF axis.

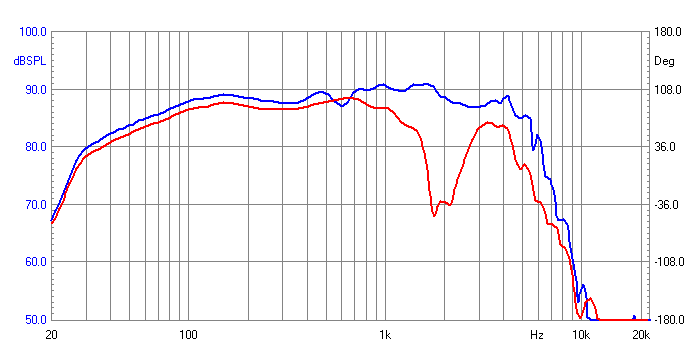
1 Metre OFF Axis Farfield Responses - Blue is Mid-Bass & Red is Bass

Again Blue Line the upper drivers as a point source and Red Line are the bottom drivers.

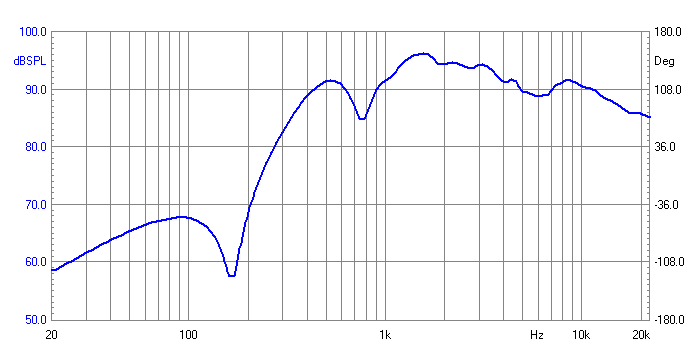
Tweeter OFF Axis Response

The Tweeter rolls of above 10KHz as is normal and there is a slight loss of energy 6Khz. But much experimentation with DW made it clear this was the best over-all compromise. The horn loading is more pronounced to a higher frequency but nothing to worry about. The 750 Hertz dip is consistent both on and off axis.

These will fill in our responses below a few hundred Hertz. Note that Nearfield measurement will not be required for the Tweeter. With a little lateral thinking, it can also be realised that we really only need to measure one of the Mid/Bass drivers.

When a Nearfield measurement is made the response is regard as a 2Pi response. As we have discussed earlier, the Diffraction Loss (DF) will be above a few hundred Hertz, so our Farfield responses above have already captured the DF and thus the Nearfield comes in below that point. In fact our first response graph shows the loss is arrested by 250 Hertz.

Nearfield measurements mean the Mic is put within 1/11^th of the effective diameter of the cone. So it a cone is 110mm in dimater, then the Mic must be no further away that 10mm. In most cases I put the Mic about 5-6mm from the cone, or in the case of drivers 8 inches or large, about 10mm from the cone.

The response graph is then adjusted using this formula:

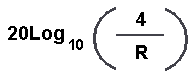
The result will be in the minus and will be in dB, where R is the effective Radius in Metres. Our driver is 133mm so R = 0.0665 – and a calculator will give us –35.6dB. I do reduce the output to the speakers by minus 10dB (so as to lessen the possible overload on the Mic) and also since the drivers are in series we also adjust for +6dB, hence the correction is –31.6dB.

Also the Port needs to be Nearfield measured as well. Again use the Radius of the Port and do the same calculation. We get the following Nearfield and Farfield (in this case ON axis):

Three Separate Measurements to be Combined

As a rule I take it as granted that any data above 500 Hertz are invalid in Nearfield measurements. We can see that Farfield (Blue) and Nearfield of the driver (Red) converge at a desirable 250 Hertz, which is where they will be joined. But before we can do that we have to sum the Port response (Green) with the Nearfield. The shelving at that point indicates that Diffraction Loss has levelled out

Cliowin used to capture these measurements allow us to perform these functions. Here are the final results:

Combined "Top" Responses, Blue is ON Axis and Red is OFF Axis.

Here is the same for the bottom drivers:

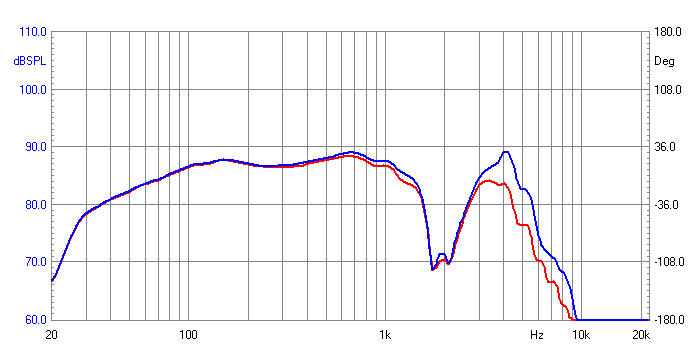
Combined "Bottom" Responses, Blue is ON Axis and Red is OFF Axis.

The Blue response is the complete ON axis and Red is OFF axis. The 2Khz dip moves up to 4-5Khz in actual use where the response will be about –20dB and hence will have no more than 1dB affect on the total response. In fact it may be helpful in suppressing the near 4Khz driver peak.

These are far simpler. We really only need two as the pairs of drivers in series are both the same (I checked) and then there is the Tweeter:

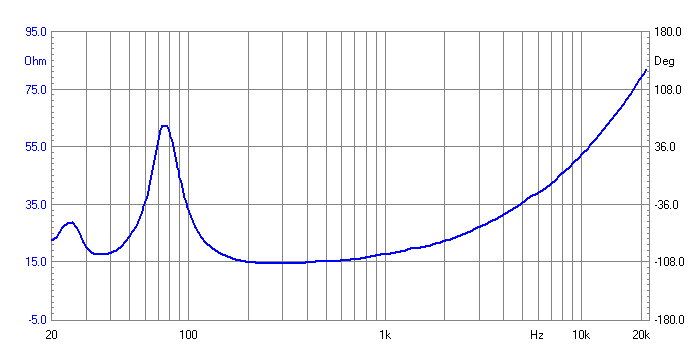
The Bass/Mid drivers measure like a single 16 Ohm driver and barely drop below 15 Ohm, just as we expected. You can also clearly see the saddle at 35 Hertz. This is the frequency the box ended up tuned to. Of course it is easy to change this tuning by varying the length of our Port. This can be experimented with later.

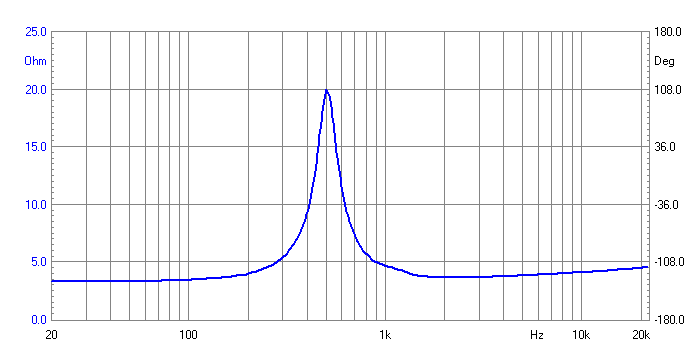
The 500 Hertz resonance is clearly shown. The Vifa XT25 Tweeter does not use ferrofluid damping and hence the prominent peak. I believe this to be an advantage, besides it has been my experience that ferrofluid damping increases the frequency of resonance (FS) and I prefer not. It also means that you have to deal with that peak in the electrical domain. It is here we have a neat solution for the XT25 Tweeter, which will be revealed here (later).

In the above electrical measurement, the DC resistance of the wiring probes were measured when shortened and that was subtracted to give above accurate results.

Note the 4Khz peak in the response. At first one might thing this is some kind of resonance and in a sense it is. But no more than the box tuning is a resonance and that vented alignment has no less than three resonant frequencies. We use these to good effect and thus not all resonant behaviour is destructive. So let us examine this 4KHz peak by using time slicing – or Waterfall plots as it has become known.

We take the pulse of one of the Mid/Bass (upper) drivers, ON axis and window it:

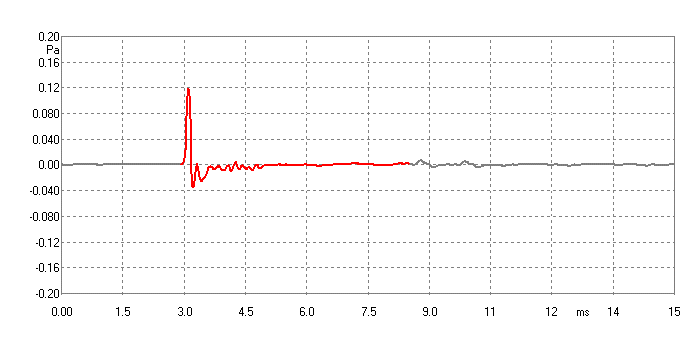
The window edits out the delay (otherwise the top of the Waterfall plot will be flat) and the main (first) reflection from the floor. The window is 5.6mS and that means meaningful data down to 178 Hertz. But we are really interested in what is happening at 4KHz. So we will now covert the pulse to Waterfall:

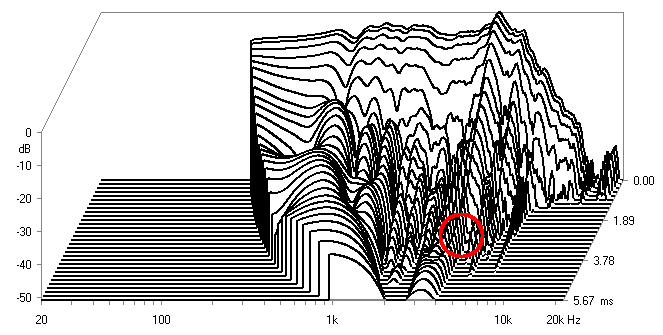
What I see is no severe resonant behaviour and the Red Circle shows it dying faster than minor irregularities at 5.3KHz and 7.2Khz. I see this, not as a cone resonance, but as a pressure point caused in a similar way to diffraction effects that you get when mounting a driver on a Front Panel, where the flushness and the shape of the baffle increases pressure at certain frequencies and not others. In my previous experience, this means we can deal with the peak in the response in a more benign ways. In the electrical domain we can flatten out the peak. What is meant by electrical domain? The Crossover.

This will lead into our next month’s Part Six. But this last plot has also indicated that my plan for the Crossover is well on track:

So here I will publish the provisional Crossover with the values shown as the design now stands (they may be subject to further tweaking).

(OLD OBSOLETE CROSSOVER BELOW)

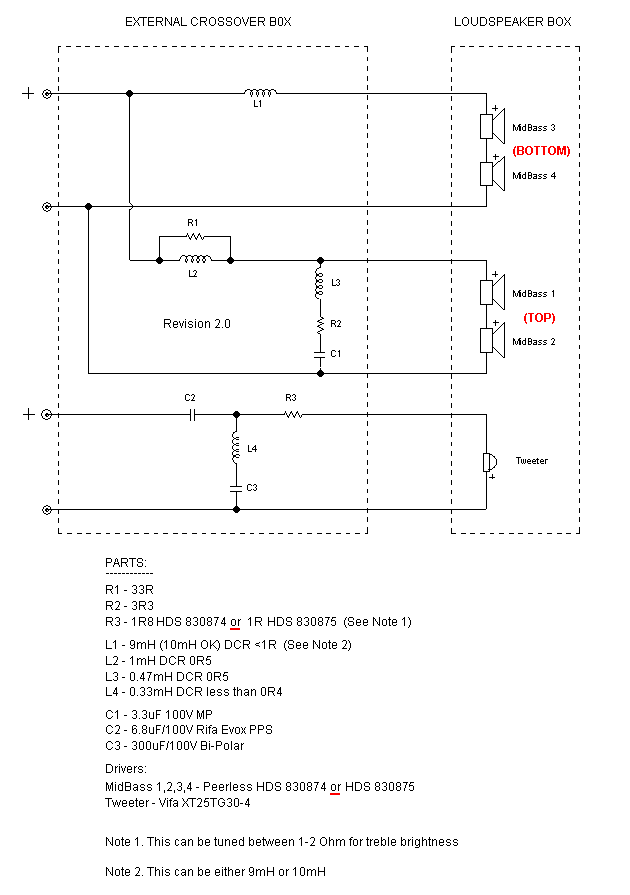
We shall revisit the Crossover in Part Six. But the combination of L3, R2 & C1 is the 4Khz trap. Also L4 & C3 sucks out the Tweeter’s 500 Hertz resonance, but also provides a High Order High Pass in the octave above that, despite the fact it is first order (quite a trick, well worth revealing in next instalment). These two ‘networks’ are critical to the performance of the Elsinores.

In the above Schematic, Mid/Bass 1 & 2 are the top two drivers (part of the Point Source). The Mid/Bass 3 & 4 are the bottom drivers. The top drivers are rolled of at their natural rate near 3-4KHz and the bottom drivers are gradually rolled of from about 200 Hertz at less than first order 6dB/Octave. In fact a first order filter will be 20dB per decade but in our case it is about 15dB per decade. The rising inductances of the drivers is not cancelled out by any Zobel Network as usual. There are reasons for this, but will also be covered in next instalment.

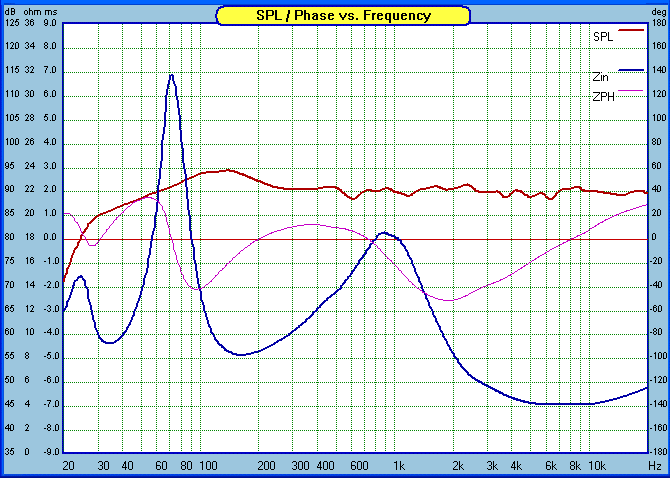
Final Modelled Response

More photos of work in progress - see Construction Photos

Next: Notes On Computer Modelling

Total Design Responsibility, Joe Rasmussen of Custom Analogue Audio & JLTi

Part Financial Sponsor & Prototype Box Construction, Bernard Chambers of Sutherland

Sounding Boards, Michael Lenehan of Lenehan Acoustics & Brad Serhan of Orpheus Loudspeakers